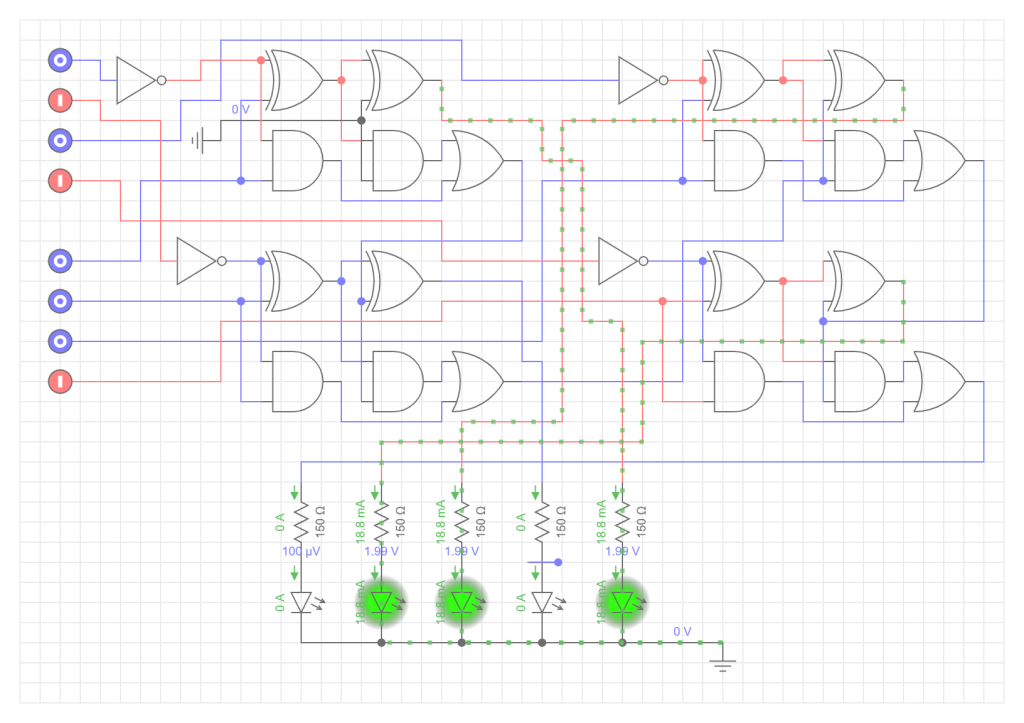
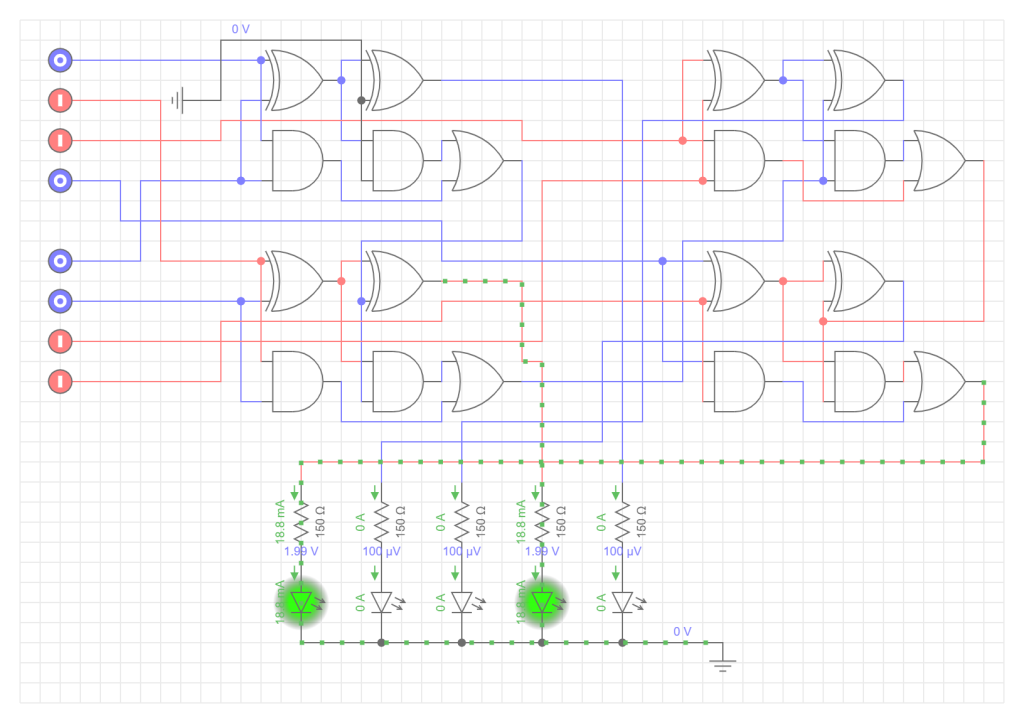
在之前，我们尝试使用逻辑门搭建了半加器、全加器，并尝试实现了一个四位二进制数加法器，这一章我们继续来研究CPU的另一个运算：减法运算。

计算机中负数的表示

众所周知，计算机中的数字是以二进制存在的，比如4对应二进制码0100，5对应二进制码0101，实际上，在计算机中会使用到一种叫“补码”的东西来表示一个数字的符号。在补码表示法中，最高位为符号位，符号位为1则该数字为负数，否则为正数。比如-5对应的二进制表示法为1011。

因为符号会占用一位，所以实际上有符号的数字(signed number)能表示的范围会比无符号的数字(unsigned number)更大。同样的，因为引入了这个概念，一个二进制数在有符号的模式和无符号的模式下可以表示两个不同的数字，比如1011在signed模式下表示-5，在unsigned模式下表示11。

实际上，除了补码表示法以外，还有其他用于表示负数的方法，不过现在用的做多的还是补码表示法，所以就不在过多介绍其他的了。

那么我们详细了解一下补码。

除了刚才所说的，补码除了最高位用作符号位以外，在负数的数字表示上也与正数不同。比如我上面举的例子，5对应的二进制码是0101，而-5并非只是把最高位置1(1101)，而是变成了1011。实际上，这是需要进行计算的。

以8位二进制数为例，二进制数的每一位上的数字有以下对应关系：

二进制位数	最高位(8)	7	6	5	4	3	2	1
十进制值	128	64	32	16	8	4	2	1

比如我们刚才计算的5，二进制为0101，就可以通过0+4+0+1=5得到，同样，如果要把01101101转换成十进制数，计算0+64+32+0+8+4+0+1=109。这就是二进制到十进制的转换法。

那么对于负数，我们也只需要将最高位的十进制值置为负数即可，比如上面的表格如果要改成signed number，对应的就是下表：

二进制位数	最高位(8)	7	6	5	4	3	2	1
十进制值	-128	64	32	16	8	4	2	1

如果我们要得到-5，只需要计算-128+64+32+16+8+0+2+1=-5即可。同样，以这种方法表示的二进制数11010111换算成十进制数就是-128+64+0+16+0+4+2+1=-41。

不仅对8位二进制数的表示法是这样，其他的也是，比如四位signed二进制数最高位表示的就是-8。

相反数计算

知道了计算机中负数的表示方法以后，我们可以想办法来计算相反数。

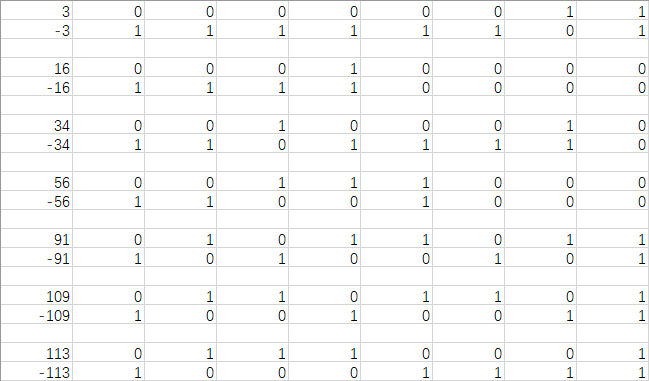
首先我们可以观察规律，我们随便选一组(signed8位二进制)数字，比如3,16,34,56,91,109,113，我们通过表格来把所有数字和对应相反数的二进制数列出来：